February 2025 Practical Practices
In our Practical Practices section of the newsletter, we highlight practices that you can incorporate in your classrooms, including curated links to outside resources to build your knowledge of that practice. For this school year CCTM has been elevating the High Leverage Teaching Practices from Principles to Action and resources to support that practice.
This month we focus on the next three practices in flow of planning for and implementing high quality math learning experiences for each student:
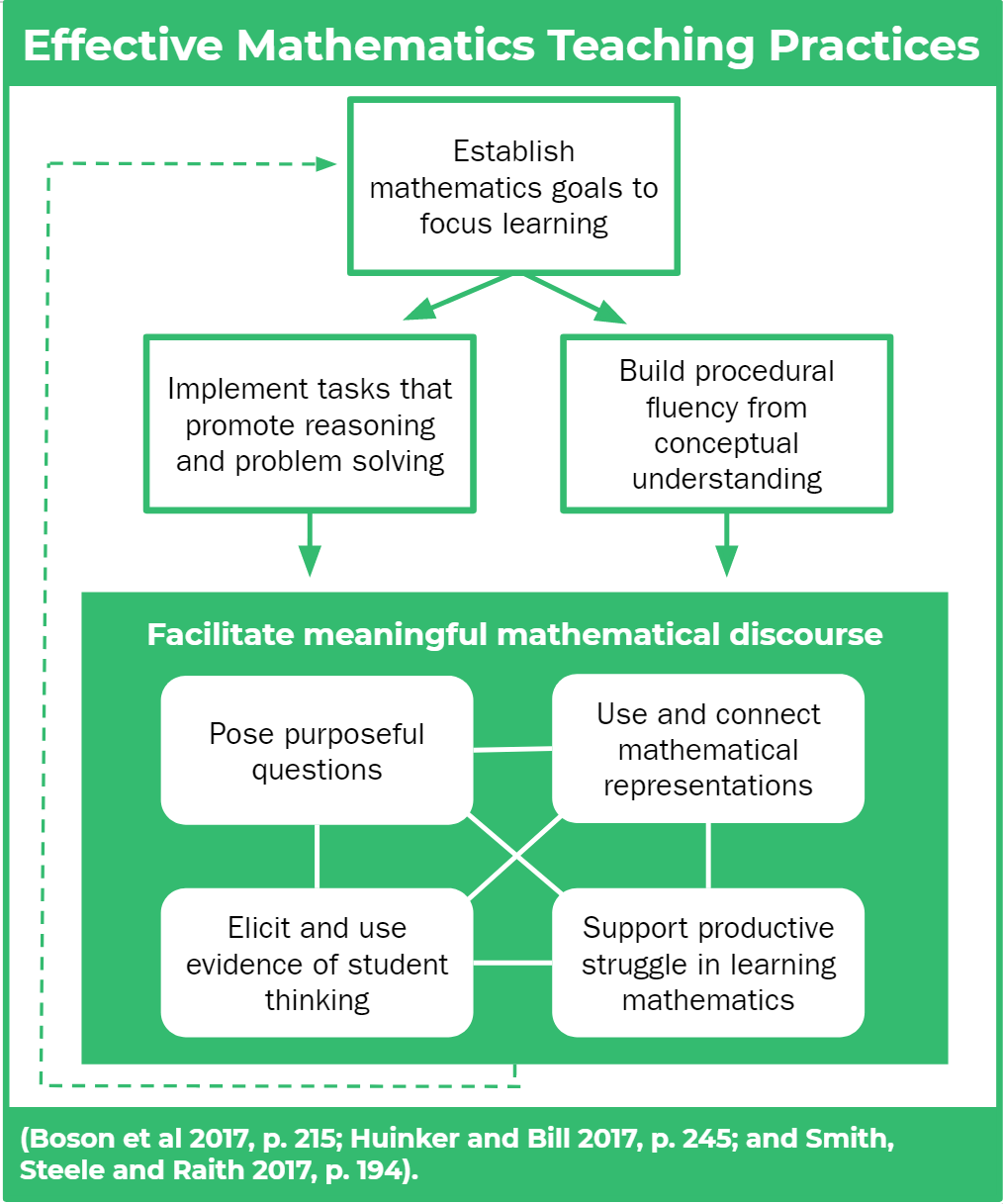
Use and connect mathematical representations.
|
|
Teacher Actions
|
Student Actions
|
-
Selecting tasks that allow students to decide which representations to use in making sense of the problems
-
Allocating substantial instructional time for students to use, discuss, and make connections among representations
-
Introducing forms of representations that can be useful to students
-
Asking students to make math drawings or use other visual supports to explain and justify their reasoning
-
Focusing students attention on the structure for essential features of mathematical ideas that appear, regardless of the representation
-
Designing ways to elicit and assess students abilities to use representations meaningfully to solve problems
|
-
Using multiple forms of representations to make sense of an understand mathematics
-
Describing and justifying their mathematical understanding and reasoning with drawings, diagrams, and other representations
-
Making choices about which forms of representations to use as tools for solving problems
-
Sketching diagrams, to make sense of problem situations
-
Contextualizing mathematical ideas by connecting them to real world situations
-
Considering the advantages or suitability of using various representations when solving problems
|
|
Dig in more!
|
Why Check it Out
|
|
Connecting Representations Routines (MP7)
|
Grace Kelemanik and Amy Lucenta explore routines to support educators in connecting representations.
|
|
Room to Grow Podcast
Mathematical Representations
|
In this episode of Room to Grow, our hosts discuss the importance of mathematical representations for students' deep learning of mathematics. The five representations described in NCTM's Principles to Actions include Physical, Visual, Symbolic, Verbal, and Contextual. Research shows that attending to and making connections between these multiple representations.
|
Facilitate Meaningful Mathematical Discourse
|
|
Teacher Actions
|
Student Actions
|
-
Engaging students and purposeful sharing of mathematical ideas, reasoning, and approaches, using varied representations.
-
Selecting and sequencing student approaches and solution strategies for whole class analysis and discussion.
-
Facilitating discourse among students by positioning them as authors of ideas, who explained and defend their approaches.
-
Ensuring progress toward mathematical goals by making explicit connections to student approaches and reasoning.
|
-
Presenting and explaining ideas, reasoning, and representations to one another impaired, small group, and whole class discourse
-
Listening carefully to and critiquing the reasoning of peers, using examples to support the counter examples to refute arguments.
-
Seeking to understand the approaches used by peers by asking, clarifying questions, trying out others strategies, and describing the approaches used by others.
-
Identifying how different approaches to solving a task are the same and how they are different
|
|
Dig in more!
|
Why Check it Out
|
|
Formative Five (book)
|
Five very doable ways to support student discourse. You can use one or all five.
|
|
Room to Grow Podcast
Routines for Supporting Student Thinking
|
In this episode of Room to Grow, Grace Kelemanik and Amy Lucenta join Curtis and Joanie to talk about how routines can provide the “opportunity and support for each and every student to develop mathematical thinking and reasoning.”
|
Pose Purposeful Questions
|
|
Teacher Actions
|
Student Actions
|
-
Advancing student understanding by asking questions that build on, but do not take over or funnel, Student thinking.
-
Making certain to ask questions that go beyond gathering information to probing thinking and requiring explanation and justification.
-
Asking intentional questions that make the mathematics more visible and accessible for student examination and discussion.
-
Allowing sufficient wait time so that more students can formulate and offer responses.
|
-
Expecting to be asked to explain, clarify, and elaborate under their thinking.
-
Thinking carefully about how to represent their responses to questions clearly, without rushing to respond quickly.
-
Reflecting on and justifying their reasoning, not simply providing answers
-
Listening to, commenting on, and questioning the contributions of their classmates.
|
|
Dig in more!
|
Why Check it Out
|
|
Using questions to stimulate mathematical thinking
|
Good questioning techniques have long being regarded as a fundamental tool of effective teachers. Unfortunately, research shows that 93% of teacher questions are "lower order" knowledge based questions focusing on recall of facts (Daines, 1986). Clearly this is not the right type of questioning to stimulate the mathematical thinking that can arise from engagement in open problems and investigations.
|
|
Rounding Up: An MLC Podcast
Posing Purposeful Questions
|
Educational theorist Charles Degarmo once said, “To question well is to teach well. In the skillful use of the question more than anything else lies the fine art of teaching.” Dr. DeAnn Huinker, author of Taking Action: Implementing Effective Mathematics Teaching Practices in Grades K-5, talks about the art and the science of questioning and ways that teachers can maximize the impact of their questions on student learning.
|

|

